
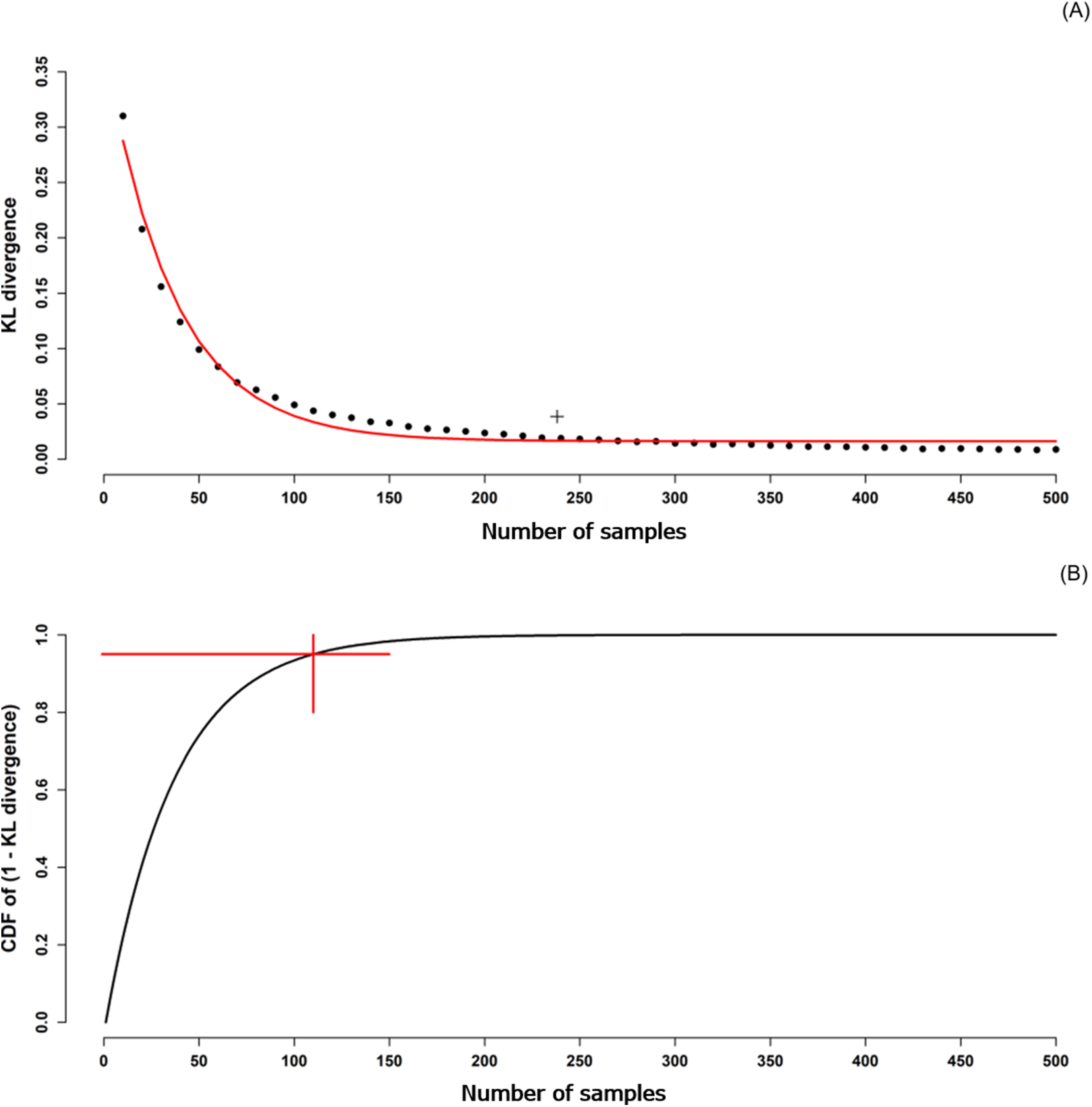
Thus, orthogonal sampling ensures that the set of random numbers is a very good representative of the real variability, LHS ensures that the set of random numbers is representative of the real variability whereas traditional random sampling (sometimes called brute force) is just a set of random numbers without any guarantees. All sample points are then chosen simultaneously making sure that the total set of sample points is a Latin hypercube sample and that each subspace is sampled with the same density. In orthogonal sampling, the sample space is divided into equally probable subspaces.Such configuration is similar to having N rooks on a chess board without threatening each other.

In Latin hypercube sampling one must first decide how many sample points to use and for each sample point remember in which row and column the sample point was taken.One does not necessarily need to know beforehand how many sample points are needed. In random sampling new sample points are generated without taking into account the previously generated sample points.

In two dimensions the difference between random sampling, Latin hypercube sampling, and orthogonal sampling can be explained as follows: Another advantage is that random samples can be taken one at a time, remembering which samples were taken so far. This sampling scheme does not require more samples for more dimensions (variables) this independence is one of the main advantages of this sampling scheme. When sampling a function of N, to be equal for each variable. A Latin hypercube is the generalisation of this concept to an arbitrary number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane containing it. In the context of statistical sampling, a square grid containing sample positions is a Latin square if (and only if) there is only one sample in each row and each column.
Conditioned latin hypercube sampling manuals#
Detailed computer codes and manuals were later published. An independently equivalent technique was proposed by Eglājs in 1977. LHS was described by Michael McKay of Los Alamos National Laboratory in 1979. The sampling method is often used to construct computer experiments or for Monte Carlo integration. Latin hypercube sampling ( LHS) is a statistical method for generating a near-random sample of parameter values from a multidimensional distribution.


 0 kommentar(er)
0 kommentar(er)
